generated with: https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html, please feel free to explore!

A simple 2-way B+ tree

assumptions:

• non-decreasing order and max degree of 3
• elements(N) are 1, 2, 3, 4, 5
• **sibling pointers (B-link borrowed)

Insertion

Inserting, find target leaf and insert the keys 1 and 2 target == root.

[figure 1]

When we insert key 3? we have our first overflow causing a split: 2 is promoted and contents are split in two, we recurse from the bottom up.

[figure 2] What if we add key 4 our tree looks weird doesn’t it:

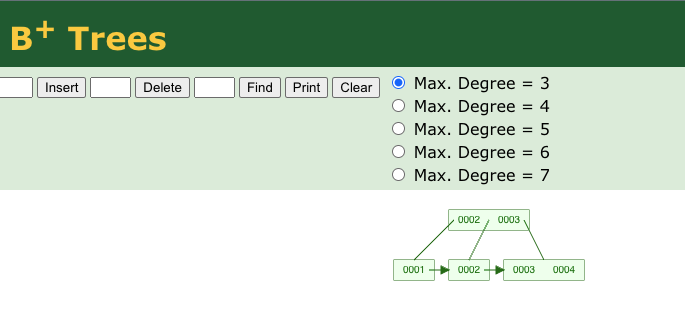
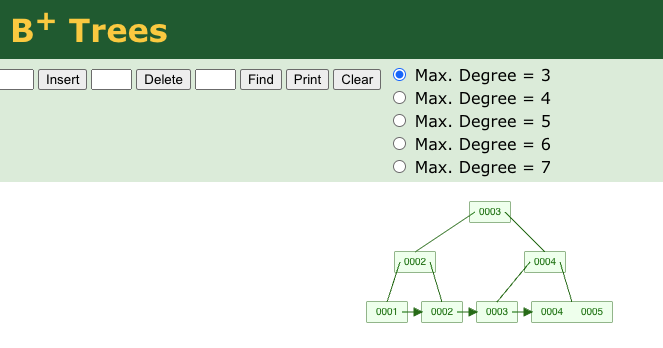
and now have to “rebalance” our tree with incoming key 5:

[figure 3]

Search

searching is an Olog(N) operation!

just a reminder this is really powerful if n = 1 billion, dominance:

• lg(n) = 0.030 μs
• f(n) = 1 sec
• nlg(n) = 29.9 sec
• n ** 2 = 31.7 years
• 2 ** n = :/

with a branching factor of 1001 and height 3 can store over one billion keys: num keys = branching factor ^ height - 1 * branching factor - 1

point and range queries follow the same logarithmic path.

[figure 4]

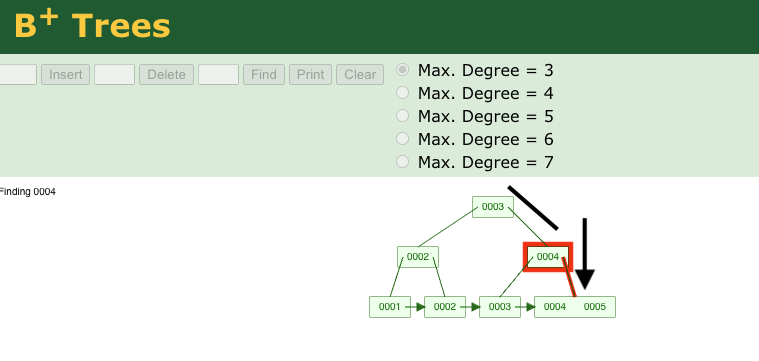
Deletion

Let’s remove 4.

First we find 4 using binary search, then re-arrange our pointers and rebalance: [figure 5]

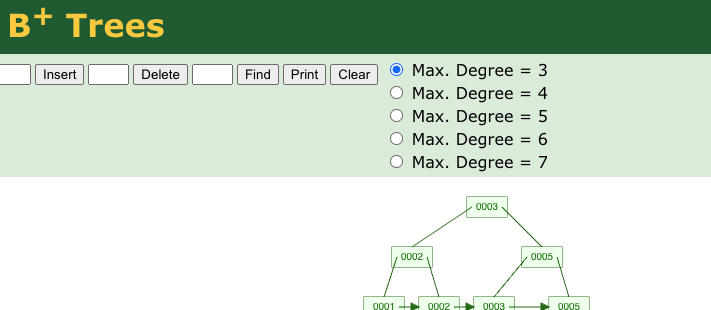
Rebalancing involves restoring our ordered structure and keeping pointers valid and performing a merge or (*redistribution.)